Függvények ábrázolása
 Dancsó Imre,
2024. május 27.
Dancsó Imre,
2024. május 27.
Függvényábrázolás | Elsőfokú függvények | Másodfokú függvények | Abszolútérték-függvények | Törtfüggvények | Hatványfüggvények | Gyökfüggvények | Exponenciális függvények | Logaritmusfüggvények | Szinuszfüggvények | Koszinuszfüggvények | Tangensfüggvények | Kotangensfüggvények | Függvénytranszformációk
Ebben a cikkben nagyon sok függvénnyel foglalkozunk. Az egyszerűbb függvényekkel már mindenki találkozik általános iskolában. 7. osztályban megismerkedünk az elsőfokú (lineáris) függvénnyel, majd érettségiig szépen lassan megtanulunk nehezebb függvényeket is ábrázolni. Úgy gyűjtöttük össze a legfontosabbakat, hogy minden korosztály megtalálja benne a számára szükséges függvényeket. Az írásban szó lesz transzformációkról, értéktáblázatról, tippekről és találkozol olyan függvényekkel is, amikre csak az emelt szintű érettségin van szükség.
Egyszerűbb függvények
Elsőfokú függvények |
Másodfokú függvények |
Abszolútérték-függvények |
Törtfüggvények |
További függvények
Hatványfüggvények |
Gyökfüggvények |
Exponenciális függvények |
Logartimusfüggvények |
Trigonometrikus függvények
Szinuszfüggvények |
Koszinuszfüggvények |
Tangensfüggvények |
Kotangensfüggvények |
Hogyan ábrázoljuk a függvényeket koordinátarendszerben?
A függvények közül azokat, amik számokhoz rendelnek számokat (valós-valós függvények), koordináta-rendszerben szoktuk ábrázolni. Az alaphalmaz (vagy az értelmezési tartomány) elemeit az x tengelyen, a x-ekhez hozzárendelt f (x) függvényértékeket pedig az y tengelyen jelöljük. Minden (x ; y) számpár meghatároz egy pontot a koordináta-rendszerben. A pontokat megfelelően összekötve megkpajuk a függvény grafikonját.
Mikor készítsünk értéktáblázatot?
Eleinte minden függvényt értéktáblázattal tanulnak a diákok ábrázolni. Ám ez később is jól jöhet, ha mondjuk nem ismered fel ránézésre a függvény típusát a megadásából, akkor mindig jó módszer az értéktáblázat készítése.
Ilyenkor célszerű néhány olyan x esetén kiszámolni az f (x) függvényértéket, amik rácspontra kerülnek, azaz x és y koordinátájuk is egész szám. Ezután a kapott számpárokat kell ábrázolnunk a koordináta-rendszerben.
Például: f (x) = x2 + 2
Ahhoz, hogy helyesen kössük össze azt a néhány pontot, amiket az értéktáblázat alapján kaptunk,tudnunk kell, hogy melyik függvénynek milyen a grafikonja.
Könnyebb dolgod van, ha a képletéből felismered a függvény típusát, mert akkor, ha a feladat ezt külön nem kéri, megspórolhatod a számolást: értéktáblázat nélkül is ábrázolhatók a nevezetes függvények.
Most megmutatjuk neked, hogyan tudod könnyen ábrázolni ezeket a nevezetes függvényeket!
Mik a lineáris függvények, és hogyan ábrázolhatjuk őket?
Lineáris függvénynek nevezzük azt a függvényt, aminek a grafikonja egyenes (lineáris = egyenes).
A hozzárendelési szabály általános alakja: f (x) = a · x + b.
Például: f (x) = -x-3; vagy g (x) =x+2
A lineáris függvény grafikonjának jellemzői:
- Meredekség:
A függvény meredkségét a-val (vagy m-mel) jelöljük (az f (x) függvény esetén ez -1, a g (x) esetén ez 3/4 ). A meredekség azt jelenti, hogy a grafikon egyik pontjából úgy kapunk meg egy másikat, hogy jobbra 1-et és fel/le "a" egységet lépünk.
Ha a > 0, akkor felfelé, ilyenkor növekvő a függvény
Ha a < 0, akkor lefelé, ekkor csökkenő a függvény.
Ha a ≠ 0, akkor a lineáris függvényt elsőfokú függvénynek nevezzük, hiszen a változó (x) első hatványon szerepel. Ha a = 0, akkor f (x) = b konstans (azaz állandó, x-től független) függvényt kapunk, képe egy vízszintes egyenes.
Ezeket a függvényeket nulladfokú függvényeknek nevezzük.
Az egyenes az y tengelyt b-nél metszi.
Például: f (x) = -x - 3 esetén: a = -1 a meredekség és b = - 3 az y tengellyel vett tengelymetszet.
Tehát az ábrázolást kezdhetjük azzal, hogy az y tengelyen a -3-at bejelöljük, ez biztosan pontja a grafikonnak. Ezután innen lépegetünk tovább: Jobbra 1-et és le 1-et, így kapjuk meg az egyenesünk további pontjait .
Ha a meredekség nem egész, akkor ahhoz, hogy egész értékeket kapjunk, azaz rácspontokon lépdelhessünk, a következő módszert érdemes használni:
Például: f (x) =
x + 2 esetén az y tengely 2-es pontjáról indulva jobbra 4-et és fel 3-at lépve kapunk újabb pontokat. Ha g (x) =
x, akkor az origóból jobbra 2-t és le (a negatív előjel miatt) 1-et lépünk.
Szeretnéd alaposan begyakorolni az elsőfokú függvények ábrázolását? Akkor ezt a videót neked készítettük!
Heti TOP videók INGYENES tananyagok KÓDOLATLAN hétvégék Tanulási TIPPEK KÜLÖNLEGES ajánlatok
380 ingyenes tananyag!
Az egyenes arányosság grafikonja
A lineáris függvények speciális esete, ha b = 0. Ekkor az egyenes átmegy az origón. Az ilyen függvényt egyenes arányosságnak is hívjuk. Ha ugyanis fennáll x és y között, hogy y = m · x, akkor az x és y egyenesen arányos egymással.
Ez azt jelenti, hogy ahányszorosára változik x, ugyanannyiszorosára változik y. Ha már gimnazista vagy, és nagyon szeretnél lenyűgözni valakit, akkor mondhatod azt is, hogy a két mennyiség egyenesen arányos, ha az összetartozó értékpárok hányadosa állandó.
Például: f (x) = 2x; vagy g (x) =x
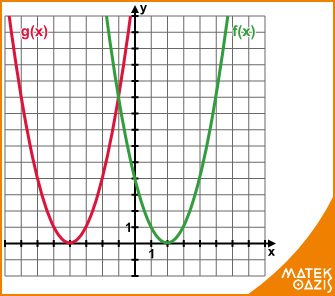
Hogyan ábrázoljuk a másodfokú függvényeket?
A legkönnyebben ábrázolható másodfokú függvény hozzárendelési szabálya f (x) = x2. A másodfokú függvények általános alakja pedig így adható meg: f (x) = a · (x + b)2 + c (ahogy olvashattad a lineáris függvényeké pedig f (x) = a · x + b).
A másodfokú függvények képe parabola.
Ha a = 1, akkor a függvény grafikonját nagyon egyszerűen az x2 függvény eltolásával kaphatjuk meg:
f (x) = x2 + c esetén az x2 függvényt „fel vagy le” kell eltolni, azaz az y tengellyel párhuzamosan. Ha c pozitív, akkor „felfelé”, ha c negatív, akkor „lefelé”.
Például: f(x) = x2 + 3 függvényt felfelé 3 egységgel; g (x) = x2 - 2 függvényt lefelé 2 egységgel
f(x) = (x - b)2 függvényt az x2 függvény x tengely mentén való eltolásával kaphatjuk meg. Jobbra kell eltolni, ha b negatív és balra, ha b pozitív.
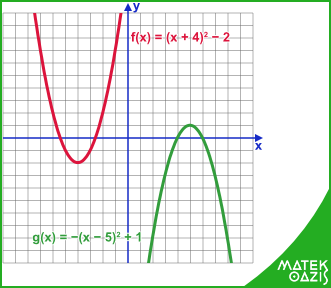
Például: f (x) = (x - 2)2 függvényt jobbra toljuk 2 egységgel; g (x) = (x + 4)2 függvényt balra toljuk 4 egységgel
Az f (x) = (x + b)2 + c függvény ábrázolásához mindkét eltolást el kell végezni:
b értéke szerint jobbra vagy balra
c értéke szerint felfelé vagy lefelé
Például: f(x) = (x + 3)2 – 2 ábrázolásakor 3 egységgel balra kell tolni az x2 függvényt, majd 2 egységgel lefelé.
Ha nem f (x) = (x + b)2 + c alakban van megadva a függvény, akkor ahhoz, hogy ábrázoljuk, először át kell alakítanunk.
Például: f (x) = x2 – 2x + 4 = (x - 1)2 + 3 (teljes négyzetté alakítottunk)
Ha úgy gondolod mindent tudsz a másodfokú függvényekről, és ezt szeretnéd is bebizonyítani, akkor neked készítettük ezt a tesztet!
Az abszolútérték-függvény, és az ábrázolása
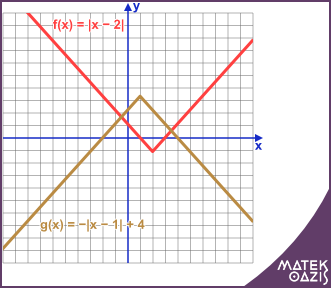
A legegyszerűbb abszolútérték függvény f (x) = | x | alakú. Az általános alakot pedig úgy írhatjuk fel, hogy: f (x) = a · | x + b | +c
Az abszolútérték-függvény grafikonja V alakú.
.png)
Általánosan elmondhatjuk, hogy egy transzformált abszolútérték-függvényt (lásd: példa) hasonlóan tudunk ábrázolni, mint egy transzformált másodfokú függvényt.
Például: f (x) = | x + 2 | - 1 esetén ugyanolyan eltolásokat kell végezni, mint a másodfokú függvény esetén, azaz 2 egységgel balra, majd 1 egységgel lefelé kell eltolni az |x| függvény grafikonját
Bizonyosodj meg arról, hogy alapos a tudásod! Nézz bele ebbe az Abszolútérték-függvény teszt-be.
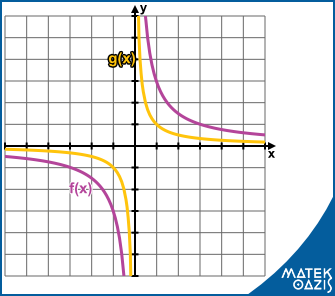
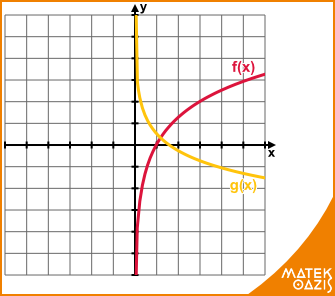
Lineáris törtfüggvény és a fordított arányosság függvénye
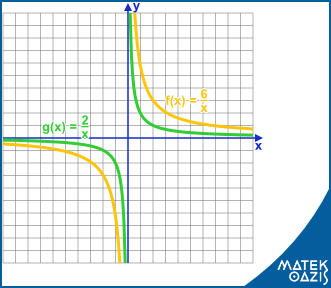
Az alapfüggvény f (x) = alakú. Általánosabban f (x) =
.
Ezt fordított arányosság függvénynek is hívjuk. Azt mondjuk, hogy két mennyiség fordítottan arányos, ha az egyik ahányszorosára nő, a másik annyiad részére csökken.
Hiszen ha x és y között fennáll az kapcsolat, akkor ez egyenértékű azzal, hogy szorzatuk állandó: x · y = a.
Emlékeztető: Két mennyiség fordítottan arányos, ha a szorzatuk állandó.
Például: f (x) =
; g (x) =

Hatványfüggvény és ábrázolása
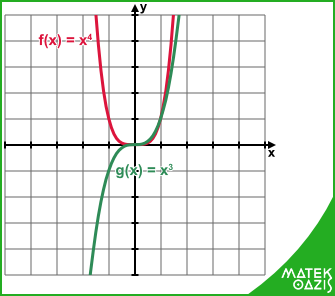
Erre már láttunk példát, hiszen az f (x) = x2 függvény is egy hatványfüggvény. Ezeknek a függvényeknek az általános alakja: f (x) = a · xn + b, ahol n egy egész szám, a és b pedig valós számok. Alapvetően érdemes két fajta hatványfüggvényt megkülönböztetni. Az egyik fajta, amikor n páros, a másik pedig, amikor n páratlan.
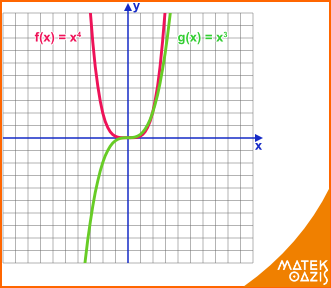
Ha n páros, akkor az x2 függvényhez nagyon hasonló grafikonokat kapunk.
Ha n páratlan, akkor kicsit más lesz a grafikon. Az y tengelytől balra eső része lefelé fog nyílni. Érdemes eleinte értéktáblázattal dolgozni. Az alábbi példák segítenek, hogy ezt jobban átlásd:
Például: f (x) = x4 g (x) = x3
A további transzformációk ugyanúgy működnek ezeknél a függvényeknél is, mint a másodfokú függvénynél.
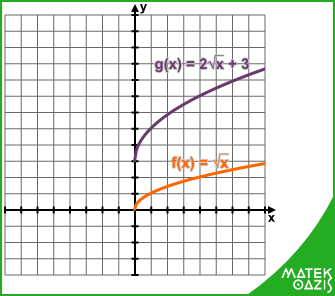
Gyökfüggvény és ábrázolása
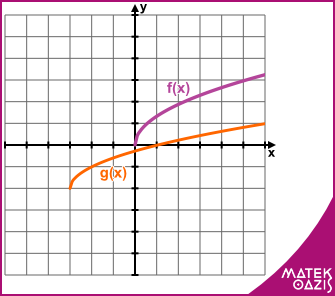
A legegyszerűbb gyökfüggvény az f (x) = √x Az általános alak az eddigi függvényekhez nagyon hasonló: f (x) = a ·√x+b + c. Az transzformációk az ábrázolásban úgy jelennek meg, mint eddig, mutatunk két egyszerű példát:
Például: f (x) = √x g (x) = √x+3 - 2
Csináltunk egy tesztet, amivel le tudott ellenőrizni, amit a gyökfüggvényről és a törtfüggvényről tanultál!
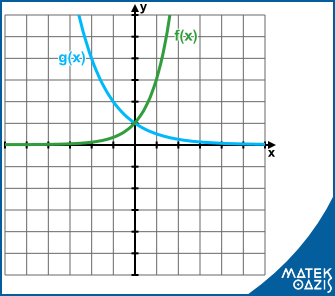
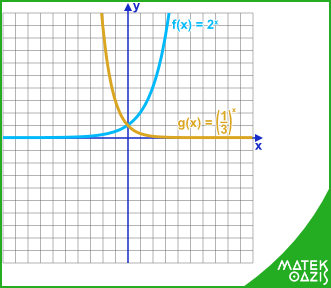
Exponenciális függvény és ábrázolása
Az exponenciális függvény hozzárendelési szabálya: f (x) = nx
Az ábrázolásnál jelölünk két-három pontos értéket és ezeket ügyesen összekötjük, figyelve a függvény főbb jellemzőire. Ebben segítenek a hatványozás tulajdonságai:
- mivel n0 = 1 minden a > 0 esetén, ezért mindegyik exponenciális függvény a 0-nál az egyet veszi fel azaz a grafikonjának pontja a (0;1) pont;
- n1 = n, vagyis x = 1 esetén n az érték, tehát a grafikonnak pontja az (1 ; n) pont;
- érdemes például az x = 2-nél felvett értéket is pontosan ábrázolni: ez lesz a (2; n2) koordinátájú pont;
- mivel n · x > 0 minden valós x és minden n > 0 esetén, ezért a grafikon a felső félsíkban helyezkedik el;
Mutatunk erre is két példát:
Például: f (x) = 3x g (x) =
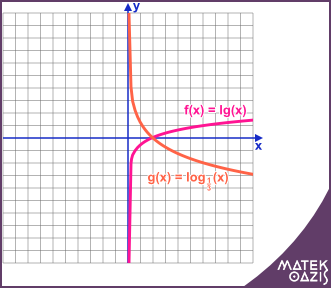
Logaritmusfüggvény és ábrázolása
A logaritmusfüggvény hozzárendelési szabálya: f (x) = logbx. (ahol b > 0; b ≠ 1; x > 0)
A logaritmus-függvény ábrázolásánál is elegendő néhány pontos értéket megkeresnünk a koordináta-rendszerben, majd ezeket megfelelően összekötni. Ebben segítenek a logaritmus-azonosságok:
- mivel logb1 = 0 minden a esetén, ezért a logaritmus-függvénynek x = 1 helyen zérushelye van;
- mivel logbb = 1 tetszőleges b esetén, ezért a logaritmus-függvénynek grafikonjának pontja a (b;1) pont;
- mivel x > 0, ezért csak a jobb félsíkban lesz ábránk.
Ugyanúgy, mint az exponenciális függvénynél, az alapon múlik, hogy a logaritmus-függvény nő vagy csökken: b > 1 esetén szigorúan monoton nő, 0 < b < 1 esetén pedig szigorúan monoton csökken. Nézzünk két példát:
Például: f (x) = log2x g (x) = log1/3 x
Tudj meg még többet az exponenciális- és logaritmusfüggvényekről!
Trigonometrikus függvények ábrázolása
Minden trigonometrikus függvény esetén érdemes nevezetes pontokat keresni, ezeket jelölni, és ügyesen összekötni. Az összekötést segítik a függvényjellemzők. Ne ijedj meg! Hasonlóan az exponenciális- es logaritmus-függvény grafikonjához, most sem az a cél, hogy milliméter-pontosságú ábrád legyen. A cél, hogy néhány nevezetes pont a helyén legyen – miután ezeket precízen bejelölted, elég, ha szépen, ívesen összekötöd őket.
Praktikus jótanács az ábrázoláshoz: Ha méretarányosan és precízen szeretnéd a grafikont elkészíteni, akkor négyzetrácsos füzetben az x-tengelyen 6 egységnél jelöld a π értékét, a függőleges y-tengelyen pedig 2 egység érjen 1-et. Így a nevezetes értékek könnyen megkereshetőek, jelölhetőek, mert rácspontok lesznek
Trigonometrikus függvények ábrázolásakor a függvénytranszformációk egészen hasonlók lesznek, mint mondjuk a másodfokú függvény esetén. Mind a négy trigonometrikus függvény esetén mutatunk majd erre példákat.
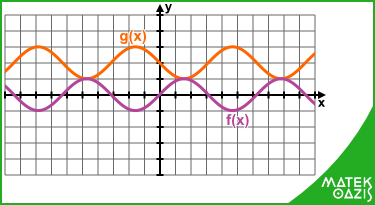
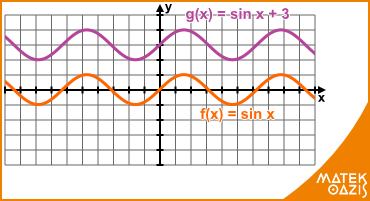
Szinuszfüggvény
A szinusz függvény nevezetes pontjai a következők:
zérushelyek: x = k · π (k ∈ ℤ)
maximum helyek: x = π / 2 + k · 2π (k ∈ ℤ)
maximum értékek: y = 1
minimum helyek: x = 3π / 2 + k · 2π (k ∈ ℤ)
minimum értékek: y = - 1
Például: f (x) = sin (x) g (x) = sin (x + π) +2
A szinuszfüggvény 2π szerint periodikus, ami azt jelenti, hogy ha megrajzolod az x tengelynek egy 2π hosszúságú szakaszán (például 0 és 2π között), akkor ezt a görbét kell csak ismételgetned ábrázoláskor.
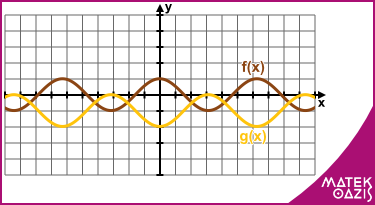
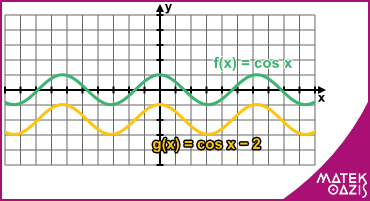
Koszinuszfüggvény
A koszinuszfüggvény grafikonja nagyon hasonlít a szinusz-görbére, sőt, pontosan úgy kaphatjuk meg, hogy a szinusz-függvény grafikonját az x tengely mentén π/2-vel balra toljuk. Ez a szoros kapcsolat megkönnyíti a dolgunkat, hasonló az ábrázolás technikája, mint a szinusz függvény esetén.
A gyakorlati jótanácsok így megegyeznek az ott leírtakkal, viszont az eltolás miatt módosulnak a nevezetes pontok:
zérushelyek: x = π / 2 + k·π (k ∈ ℤ)
maximum helyek: x = k · 2π (k ∈ ℤ)
maximum értékek: y = 1
minimum helyek: x = π + k · 2π (k ∈ ℤ)
minimum értékek: y = -1
Például: f (x) = cos (x) g (x) = cos (x - π) -1
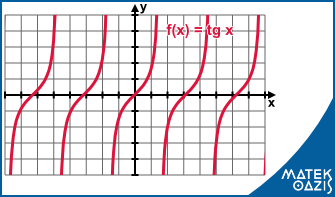
Tangensfüggvény
Kezdjük ezt a részt a tangens definíciójával:
Definíció: Ha x ∈ ℝ, x ≠ π/2+ k · π (k ∈ ℤ) , akkor
Most nézzük meg, hogy néz ki a függvény:
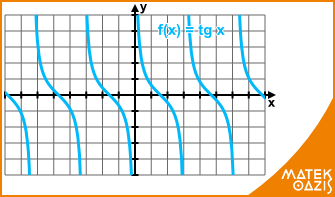
Mit látsz az ábrán, ami segíti az ábrázolást?
A kikötés, amI a definícióból kiderül: az x = π / 2 + k · π (k ∈ ℤ) alakú számok, ezeknél függőleges szaggatott vonalakat szokás rajzolni. Két-két ilyen között a tangens függvény szigorúan monoton nő, „simulva” ezekhez a szaggatott vonalakhoz (de soha nem éri el őket!). A tangens függvény zérushelyei: x = k · π (k ∈ ℤ).
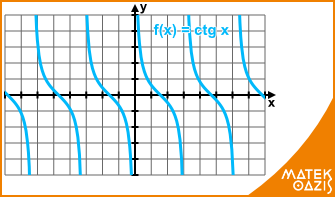
Kotangensfüggvény
Itt a kikötés miatt az x = k · π (k ∈ ℤ) értékeknél lesznek a függőleges szaggatott vonalak, ezek között szigorúan monoton csökken a kotangens függvény.
Zérushelyei: x = π / 2 + k · π (k ∈ ℤ)
Mire használjuk a trigonometrikus függvényeket? Fizikában a szinusz-függvénynek különös jelentősége van például az elektromágneses hullámoknál és a rezgéseknél. Ezekről itt olvashatsz részletesebben.
Függvénytranszformációk
Ebben a részben általánosan összefoglaljuk azokat a lehetőségeket, mozgatásokat, amik az alapfüggvénnyel történhetnek. Ezeket hívjuk függvény-transzformációknak. A rájuk vonatkozó szabályok ismerete nagyon megkönnyíti a függvényábrázolást. Összefoglalva ezeket:
1. A zárójelen belüli hozzáadás/kivonás oldalra visz (balra-jobbra mozgat)
2. A zárójelen kívüli hozzáadás/kivonás fel-le mozgatja a függvény grafikonját
3. A külső szorzó nyújt (vagy éppen ellaposítja a függvényt)
4. A belső szorzó y tengelyre merőleges irányban nyújt/zsugorít
Az első két transzformációt a másodfokú függvény kapcsány alaposan megtárgyaltuk, most nézzük részletesebben a másik két transzformációt.
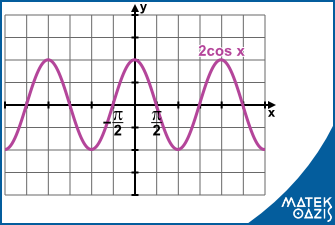
3. A külső szorzó nyújt (vagy éppen ellaposítja a függvényt)
A c · f (x) alakú függvény grafikonja az f (x) alapfüggvény grafikonjának y tengely menti nyújtásával/zsugorításával kapható meg: a görbe minden pontjának y koordinátáját c-szeresére változtatjuk.
Például: 2 · cosx
4. A belső szorzó y tengelyre merőleges irányban nyújt/zsugorít
Az f (d · x) függvény grafikonját az f (x) alapfüggvény grafikonjából úgy kapjuk meg, hogy az y tengelyre merőleges irányban d-ed részére zsugorítjuk (így d-szer közelebb kerülnek a pontok az y tengelyhez).
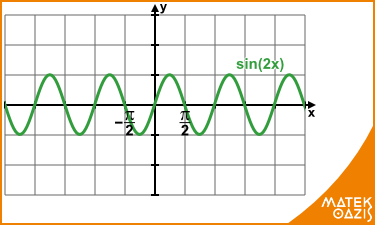
Például: sin (2x)
Sokszor olyan függvényt kell ábrázolnunk, amely az alapfüggvényből több transzformáció egymásutánjával kapható meg. Ilyenkor célszerű ezeket lépésről lépésre végrehajtani, és minden állapotot ábrázolni. Ha ezeket a grafikonokat közös koordinátarendszerben szeretnénk megrajzolni, akkor az átláthatóságot nagyban megkönnyíti a különböző színek használata.
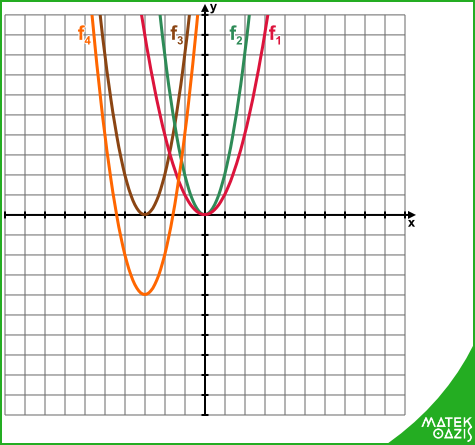
Például: f (x) = 2 · (x + 3)2 - 4
f1(x) = x2 ➝ f2(x) = 2 · (x)2 ➝ f3(x) = 2 · (x+3)2 ➝ f4 (x) = f (x) = 2 · (x + 3)2 - 4
Gyakorold be ezzel a tananyaggal, amit a függvénytranszformációkról tanultál!

Matek- és fizikatanár

Egészrész és törtrész függvény: definíció, feladatok
Mi az egészrész fogalma? Mi a törtrész fogalma? Mit kell tudni az egészrész függvényről? Mit kell tudni a törtrész függvényről?

.png)
.png)
.png)
.png)
.png)