Matematika felvételi 2024: ezek voltak a feladatok és megoldások!
 Dancsó Imre,
2024. november 28.
Dancsó Imre,
2024. november 28.
8. osztály típusfeladatok | 8. osztály interaktív feladatok | 8. osztály feladatok | 6. osztály típusfeladatok | 6. osztály interaktív feladatok | 6. osztály feladatok | 4. osztály típusfeladatok | 4. osztály interaktív feladatok | 4. osztály feladatok

8. osztály: milyen feladatok voltak?
A nyolcadik osztályosok központi írásbeli felvételije -az új követelmények ellenére- senkinek nem okozott meglepetést. Ugyanazok a típusfeladatok voltak, mint az elmúlt években. Ezek ellenére még mindig nem könnyű jól teljesíteni, hiszen az idővel való versenyfutás is megmaradt az elmúlt évekből. Nézzük milyen típusok kerültek be a feladatsorba, mire kaptak a gyerekek 45 percet!
1. feladat: Könnyű számolási feladatok (törtek, hatványozás, módusz, oszthatóság)
2. feladat: Mértékegységváltás (idén tömeg, idő, terület)
3. feladat: Kombinatorika (Összeszámlálsi feladat) (minden évben nehézség, hogy nem tudja a vizsgázó, hány megoldás van)
4. feladat: Grafikon elemzés
5. feladat: Tájékozódás koordináta-rendszerben, területszámítás
6. feladat: Szöveges feladat (arányosság)
7. feladat: Szögek meghatározása ábra alapján (egyenlőszárú háromszögek)Feleletválasztós feladatok (oszthatóság, százalék, szögek)
8. feladat: Feleletválasztós feladatok ((oszthatóság, geometria, LKKT)
9. feladat: Térgeometria (felszínszámolás)
10. feladat: Nehéz szöveges feladat (Törtes szöveges feladat)
Nézzük részletesen a feladatokat megoldásokkal együtt!
Itt megtalálod a 2024-es matematika felvételi első 5 feladatát interaktív megoldásokkal, amikből rengeteget tanulhatsz.
(Az interaktív megoldásokhoz jelentkezz be! Ha még nincs fiókod, akkor regisztrálj!)
Hasonló interaktív videókon átnézhetsz minden matek felvételi témakört, és begyakorolhatod az felvételi feladatok megoldását!
Jöhet a többi feladat? Csináld meg velünk a 2024-es matematika felvételi 6-10. feladatát!
Nézd meg a videót és közben válaszolj a kérdésekre! (Lépj be, vagy regisztrálj.)
Hihetetlenül gyorsan tudsz készülni matekból a felvételire az egyedi módszereknek és a jól felépített tananyagnak köszönhetően:
Többet szeretnék tudni a felvételi tréningről
Ezek voltak a 8.-os felvételi feladatok:
1. Határozd meg az A, B, C és D érékét!
a) A =
b) 79 · 78 = 7B
c) C = a 2; 3; 3; 4; 5; 2; 3; 3; 2; 4; 1 számsokaság módusza
d-e) D egy számjegy, amivel a 32D57 ötjegyű szám osztható 9-cel.
2. Tedd igazzá az alábbi egyenlőségeket a hiányzó mérőszámok beírásával!
a) 12 dkg + __________ g = 731 g
b) 3000 másodperc - __________ perc = 30 perc
c-d) __________ dm2 + 82 500 cm2 =1750 dm2 = __________ m2
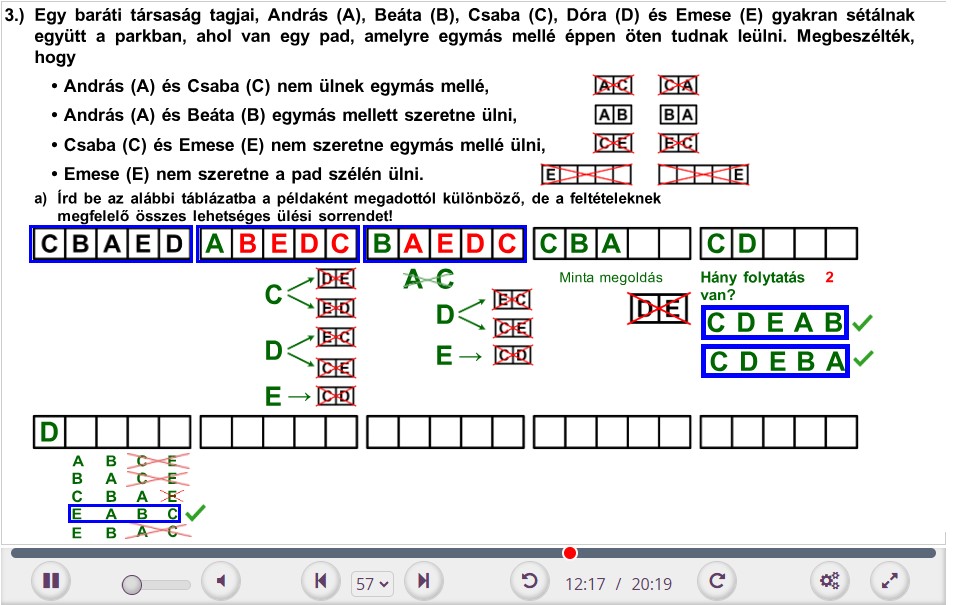
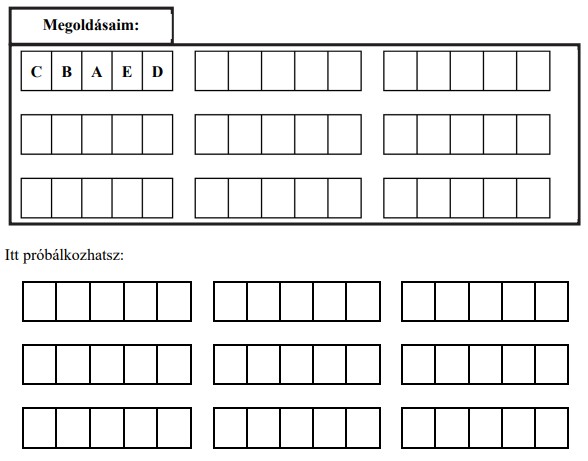
3. Egy baráti társaság tagjai, András (A), Beáta (B), Csaba (C), Dóra (D) és Emese (E) gyakran sétálnak együtt a parkban, ahol van egy pad, amelyre egymás mellé éppen öten tudnak leülni. Megbeszélték, hogy
– András (A) és Csaba (C) nem ülnek egymás mellé,
– András (A) és Beáta (B) egymás mellett szeretne ülni,
– Csaba (C) és Emese (E) nem szeretne egymás mellé ülni,
– Emese (E) nem szeretne a pad szélén ülni.
a) Írd be az alábbi táblázatba a példaként megadottól különböző, de a feltételeknek megfelelő összes lehetséges ülési sorrendet! Megoldásaidat a vastag vonallal körülvett részbe kell beírnod, mert csak ezt értékeljük. Lehet, hogy több üres ábrát adtunk meg, mint ahány megoldás van.
A példaként megadott ülési sorrendet már beírtuk. A bekeretezett rész alatti területen próbálkozhatsz, de az oda beírt megoldásokat NEM értékeljük! Vigyázz!
Ha a megoldásaid közé hibás sorrendet is beírsz, nem kaphatsz maximális pontszámot!
4. A következő diagram azt mutatja, hogy Emese hány napon gyakorolt adott számú percet a felvételire.
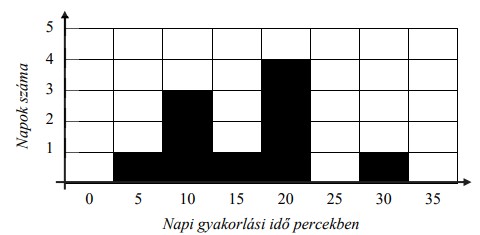
a) Hány napon gyakorolt Emese a felvételire?
b–c) Hány percet gyakorolt összesen Emese a felvételire? Írd le a számolás menetét is!
A második naptól kezdve Emese minden nap legalább annyi ideig gyakorolt, mint az előző napon.
d–e) Hány percet gyakorolt naponta átlagosan az utolsó öt napon? Írd le a számolás menetét is!
5. Az alábbi ábrán szereplő koordináta rendszerben a B (4; 2) és a D (0; 4) pont az f egyenesen helyezkedik el.
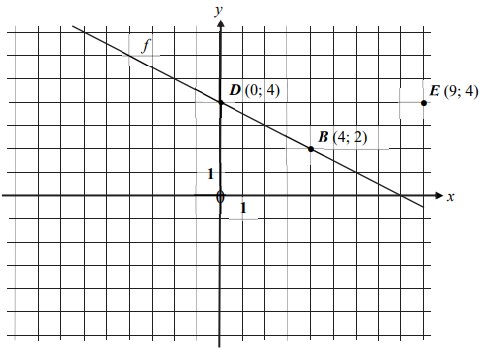
a–b) Rajzold be az ábrába az A pontot, és határozd meg az y koordinátáját!
A C pont a B pont y tengelyre vonatkozó tükörképe.
c–d) Rajzold be az ábrába a C pontot, és határozd meg a koordinátáit!
e–f–g) Határozd meg az EDB háromszög területét!
(Az ábrán látható koordináta rendszer 1 rácsnégyzetének területe 1 területegység.) Írd le a számolás menetét is!
6. A 120 gramm tömegű „HABOS” szappan ára 150 forint volt. A szappangyár megszüntette a 120 gramm tömegű „HABOS” szappan gyártását, helyette 80 grammos méretben kezdte el gyártani a „HABOS” szappant.
A 80 gramm tömegű „HABOS” szappan ára 160 forint lett.
a) Hányszorosára emelkedett a „HABOS” szappan 1 kilogrammjának az ára ezzel a változtatással? (A csomagolás árát nem kell figyelembe venned!)
Írd le a számolás menetét is!
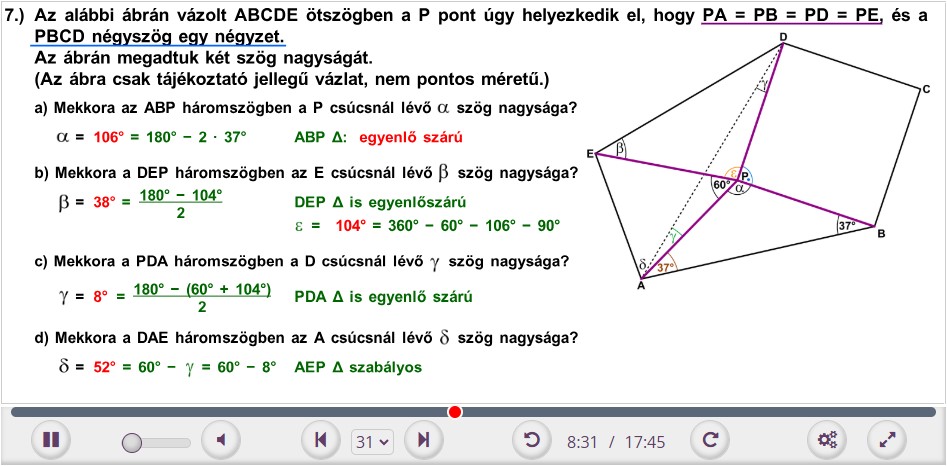
7. Az alábbi ábrán vázolt ABCDE ötszögben a P pont úgy helyezkedik el, hogy PA = PB = PD = PE, és a PBCD négyszög egy négyzet.
Az ábrán megadtuk két szög nagyságát. (Az ábra csak tájékoztató jellegű vázlat, nem pontos méretű.)
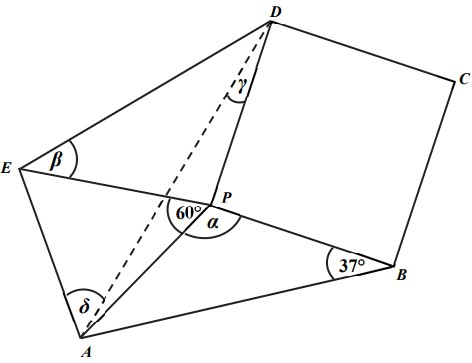
a) Mekkora az ABP háromszögben a P csúcsnál lévő α szög nagysága?
b) Mekkora a DEP háromszögben az E csúcsnál lévő β szög nagysága?
c) Mekkora a PDA háromszögben a D csúcsnál lévő γ szög nagysága?
d) Mekkora a DAE háromszögben az A csúcsnál lévő δ szög nagysága?
8. Minden kérdésnél karikázd be az egyetlen helyes válasz betűjelét!
a) Mennyi a 12 pozitív osztóinak az összege?
(A) 15 (B) 16 (C) 28 (D) 27
b) Hány cm hosszú annak a téglalapnak a rövidebb oldala, amelynek a kerülete 35 cm, a hosszabbik oldalának hossza pedig 14 cm?
(A) 21 (B) 3,5 (C) 10,5 (D) 7
(A) 180 (B) 60 (C) 120 (D) 90
d) Melyik lehet az alábbiak közül egy háromszög három oldalának hossza?
(A) 12 cm; 47,5 cm; 35,5 cm
(B) 5 mm; 13 mm; 7 mm
(C) 22 m; 33 m; 44 m
(D) 17 dm; 25 dm; 6 dm
9. Az ábrán látható háromszög alapú egyenes hasábban
a = 10 cm, b = 20 cm, c = 24 cm, d = 8 cm.
(Az ábra csak tájékoztató jellegű vázlat, nem pontos méretű.)
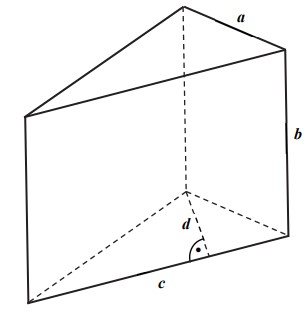
a) Hány cm3 az ábrán látható hasáb térfogata? Írd le a számolás menetét is!
10. Egy gazda a négy fia (András, Béla, Csaba, Dezső) között elosztotta a birkanyáját.
András kapta a teljes nyáj negyedét, Béla a teljes nyáj harmadát. Csaba az András és a Béla része után megmaradt birkák ötödét kapta meg. Dezső 40 birkát vihetett haza.
a) Hány darab birkából állt a gazda birkanyája?
Írd le a számolás menetét is!
Hihetetlenül gyorsan tudsz készülni matekból a felvételire az egyedi módszereknek és a jól felépített tananyagnak köszönhetően:
Többet szeretnék tudni a felvételi tréningről
6. osztály: milyen feladatok voltak?
Nem túlzás azt mondani, hogy a hatodikosok számára készített felvételi sokszor a legnehezebb a 3 közül. 45 perc jut 10 feladatra, amik nagyon nehezek a tanulók számára. Minden évben van olyan feladat, aminek megoldásához egyenlet kell, amit sok diák még nem tanult megoldani. Ezen kívül bonyolult algebrai kifejezésekkel is meg kell küzdeni. Nézzük típusok szerint mi várta a felvételizőket!
1. feladat: Műveletek elvégzése (átlagos 1. feladat. Fókuszban van a műveleti sorrend alkalmazása)
2. feladat: Táblázat adataira vonatkozó kérdések
3. feladat: Mértékegységátváltás (hosszúság, tömeg, terület, idő, űrtartalom)
4. feladat: Szöveges feladat (oszthatóság)
5. feladat: Igaz-hamis (geometria témakörben)
6. feladat: Összes eset összegyűjtése
7. feladat: Szöveges feladat (sok kérdés, hosszú szöveg)
8. feladat: Szöveges feladat (térgeometria)
9. feladat: Szöveges feladat (egyenletmegoldás)
10. feladat: Szöveges feladat (hosszú, időigényes)
Nézzük részletesen a feladatokat, megoldásokkal együtt!
Csináld velünk a 2024-es matematika felvételi első 5 feladatát interaktív megoldásokkal, amikből rengeteget tanulhatsz:
Megtetszettek az interaktív tananyagok? Rengeteg videót találsz még az oldalunkon, ami segít felkészülni, és elérni a céljaid!
Készen állsz még négy feladatra? Csatlakozz hozzánk, és oldd meg velünk a 2024-es matematika felvételi 6-10. feladatát (December 5-től)!
Az interaktív megoldásokhoz be kell jelentkezned! Ha még nincs fiókod, akkor regisztrálj!
Többet szeretnék tudni a felvételi tréningről
Ezek voltak a feladatok:
1. Végezd el a kijelölt műveleteket!
a) 4 · 248 + 6 · 248 =
b)
c) 5 · 7 – (– 2) + (– 10) =
d) 6,5 - 0,5 ∙ 4 =
e)
2.) Egy zöldségesnél háromféle déligyümölcs kapható: banán, narancs és mandarin. Az alábbi táblázat azt mutatja, hogy melyik déligyümölcsből hány kilogrammot adtak el az év első négy hetében.
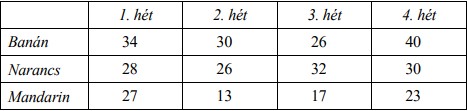
a) Melyik déligyümölcsből adták el a legtöbbet a négy hét alatt?
b) Hány olyan hét volt, amikor több banánt adtak el, mint narancsot?
c) Hány kilogrammal több mandarint adtak el az 1. héten, mint a 4. héten?
d) Hány kilogramm mandarint adtak el átlagosan hetente ez alatt az idő alatt?
3. Pótold a hiányzó mérőszámokat!
a) 3 m 40 cm - _____ cm = 2 m
b) 8 kg 30 g= __________ dkg
c) 5 dm2 + 3 m2 = __________ dm2
d) óra - __________ perc = 2 óra
e) 3 liter + __________ dl = 45 dl
4. Anna és Berci kooperatív játékot játszottak, amelyben vagy együtt nyertek vagy együtt veszítettek. A játék során egyszerre mondtak egy-egy természetes számot, és akkor nyertek, ha a két szám szorzata 36 volt. A játékot többször játszották, és meglepő módon mindig nyertek.
a) Mit mondott Berci, ha Anna 3-at mondott?
b) Sorold fel azokat az egyjegyű számokat, amelyeket Anna mondhatott a játék során!
c) Mi lehetett a legnagyobb szám, amit Berci mondhatott?
d) Mi a lehetséges legkisebb értéke az Anna és Berci által mondott két szám összegének?
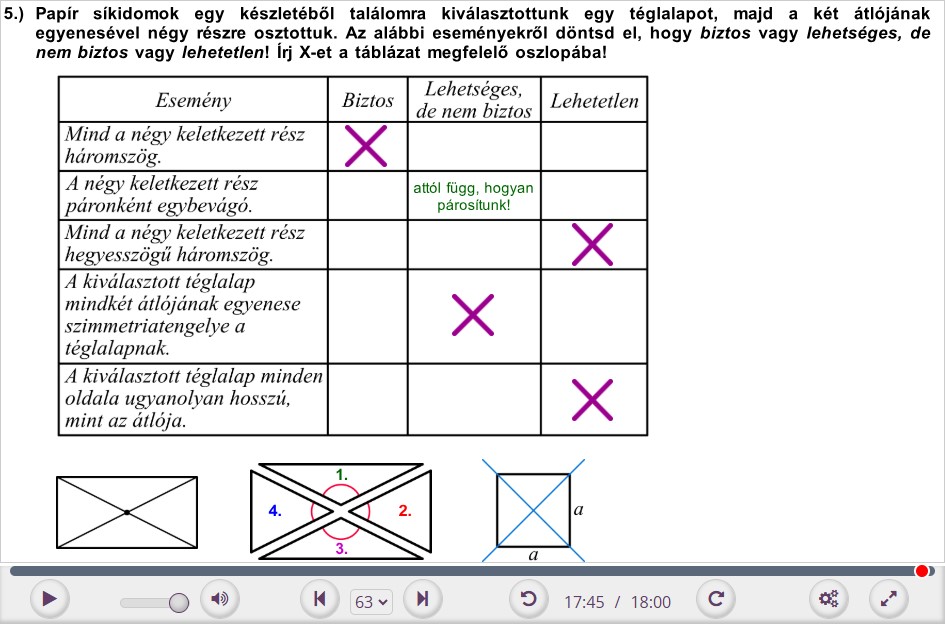
5. Papír síkidomok egy készletéből találomra kiválasztottunk egy téglalapot, majd a két átlójának egyenesével négy részre osztottuk. Az alábbi eseményekről döntsd el, hogy biztos vagy lehetséges, de nem biztos vagy lehetetlen! Írj X-et a táblázat megfelelő oszlopába!
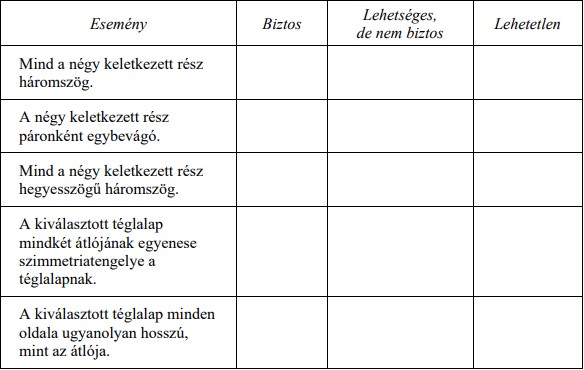
6. Sorold fel azokat a 2-vel kezdődő négyjegyű természetes számokat, amelyekre igaz, hogy a szomszédos számjegyek különbsége 2 (mindig a nagyobb számjegyből vonjuk ki a kisebbet)!
7. Az óriáskerék átmérője 50 méter, 30 kabinja van, mindegyik kabinba legfeljebb 6 fő szállhat be. Az óriáskerék 3 éves kor alatt ingyenes. Az óriáskerékre egy gyermekjegy 3 és 14 év közöttieknek 1500 Ft, diákigazolvánnyal rendelkező 14 feletti diákoknak 2000 Ft, egy felnőtt jegy 2500 Ft. Négy felnőttnek 9000 Ft a csoportos jegy, a 2 felnőttnek és 3 gyermeknek szóló családi jegy 8200 Ft. Egy 20 fős társaság 10 felnőttből és 10 gyermekből áll. Közülük 2 gyermek 3 év alatti, a többi gyermek 3 és 14 év közötti.
a) Legkevesebb hány kabinban fér el a 20 fős társaság?
b) Hány forinttal drágább 4 felnőtt jegy, mint egy csoportos jegy?
c) Hány családi jegyet kell vásárolnia a 20 fős társaságnak ahhoz, hogy a jegyekért összesen a legkevesebbet fizessék?
d) Hány forintot fizet a társaság összesen a jegyekért, ha ez az összeg a lehető legkevesebb?
8. Egy téglatest alakú szoba egyik falának mérete 5 m × 3 m, ezzel szomszédos másik falának mérete 6 m × 3 m. A szobának két ablaka van, amelyek egyformák, téglalap alakúak és méretük 1 m × 1,5 m. A szobának egy ajtaja van, amely téglalap alakú és 2 m × 2,5 m méretű.
a) Hány négyzetméter területű a plafon?
b) Hány négyzetméter az ablakok és az ajtó területének összege?
c) A szoba minden falát kitapétázzuk. Hány négyzetméter falfelületet kell tapétázni?
d) Tapétázáskor a tapétázandó területnél a tizedével nagyobb területű tapétát kell vásárolni. Hány tekercs tapétára van szükség a falak tapétázásához, ha egy tekercs területe 10 m2 ?
9. Egy főre egy étkészlet egy lapostányérból, egy mélytányérból, egy kistányérból, egy csészéből és egy csészealjból áll. Nyolc főre az étkészlet 40000 Ft. Egy mélytányér 1200 Ft. Egy lapostányér 300 forinttal többe kerül, mint egy kistányér. Egy csésze és egy csészealj együtt feleannyiba kerül, mint egy kistányér.
a) Hány forintba kerül egy főre az étkészlet?
b) Hány forintba kerül egy csésze, egy csészealj és két kistányér együtt?
c) Hány forintba kerül egy csésze és egy csészealj együtt?
d) Hány forintba kerül egy kistányér?
e) Hány forintba kerül egy lapostányér?
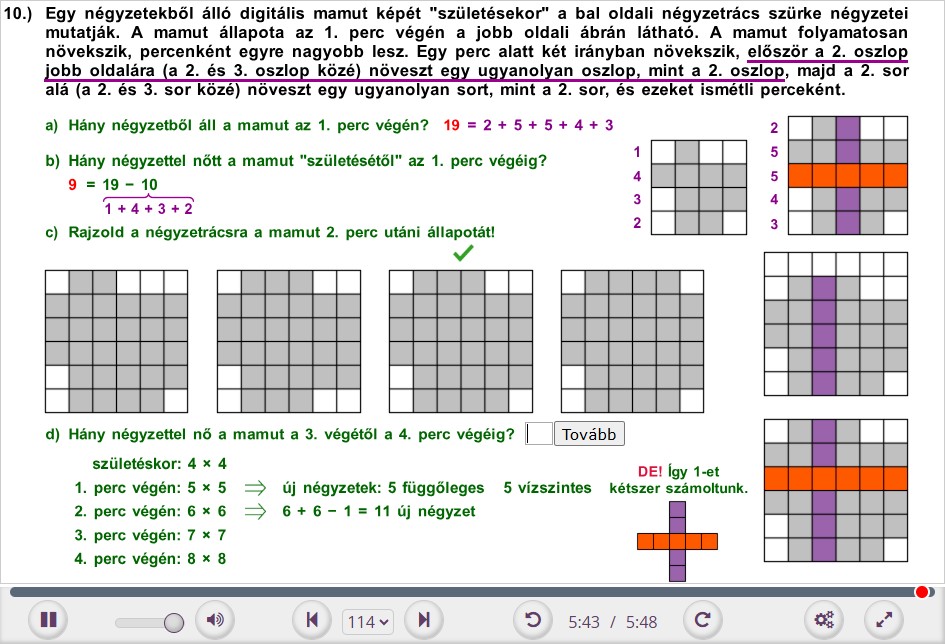
10. Egy négyzetekből álló digitális mamut képét „születésekor” a bal oldali négyzetrács szürke négyzetei mutatják. A mamut állapota az 1. perc végén a jobb oldali ábrán látható. A mamut folyamatosan növekszik, percenként egyre nagyobb lesz. Egy perc alatt két irányban növekszik, először a 2. oszlop jobb oldalára (a 2. és 3. oszlop közé) növeszt egy ugyanolyan oszlopot, mint a 2. oszlop, majd a 2. sor alá (a 2. és 3. sor közé) növeszt egy ugyanolyan sort, mint a 2. sor, és ezeket ismétli percenként.
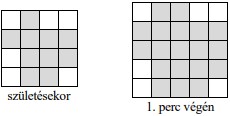
a) Hány négyzetből áll a mamut az 1. perc végén?
b) Hány négyzettel nőtt a mamut „születésétől” az 1. perc végéig?
c) Rajzold a négyzetrácsra a mamut 2. perc utáni állapotát!
d) Hány négyzettel nő a mamut a 3. perc végétől a 4. perc végéig?
Megtetszettek az interaktív videók? Képzeld minden felvételihez szükséges témakörhöz készítettünk tananyagot. Fejlődj velünk gyorsan, és írj sikeres felvételit!
Többet szeretnék tudni a felvételi tréningről
4. osztály: milyen feladatok voltak?
A negyedik osztályos felvételizőknek sincsen könnyebb dolguk, mint hatodikos és nyolcadikos társaiknak. Nagyon fiatalon, sokan talán először kerülnek versenyhelyzetbe matematikából. Fontos rutint szerezni a diákoknak mire eljutnak a felvételi megírásáig. A feladatok hasonlóak voltak 2024-ben is, mint az előző években. Mutatjuk, hogy épült fel ebben az évben a negyedikes központi matematika felvételi!
1. feladat: Egyszerű számolási feladatok (műveleti sorrend és a függőleges elrendezés okozhat nehézséget)
2. feladat: Diagram elemzés
3. feladat: Számolási feladatok
4. feladat: Logika puzzle (Összes megoldás megkeresése)
5. feladat: Logikai feladat (következtetéssel, esetkizárással))
6. feladat: Mértékegységváltás
7. feladat: Kerület, terület, szimmetria
8. feladat: Térbeli feladat (kockával kapcsolatos kérdések)
9. feladat: Hosszú szöveges feladat
10. feladat: Hosszú sormintás feladat
Nézzük részletesen a feladatokat, megoldásokkal együtt!
Készítettünk egy színes interaktív videót, amiben meg tudod velünk oldani a 2024-es matematika felvételi első 5 feladatát. Ezekből nagyon sokat tudsz tanulni, és rutint szerezhetsz a feladatmegoldásban:
Tanulj velünk interaktívan! Mi kérdezünk, te válaszolsz. Talán te is meglepődsz majd, hogy milyen gyorsan fejlődsz!
Nincs más hátra, nézzük meg a maradék öt feladatot! Tarts velünk, oldjuk meg együtt a 2024-es matematika felvételi 6-10. feladatát!
Az interaktív megoldásokhoz be kell jelentkezned! Ha még nincs fiókod, akkor regisztrálj!
Többet szeretnék tudni a felvételi tréningről
Ezek voltak a feladatok:
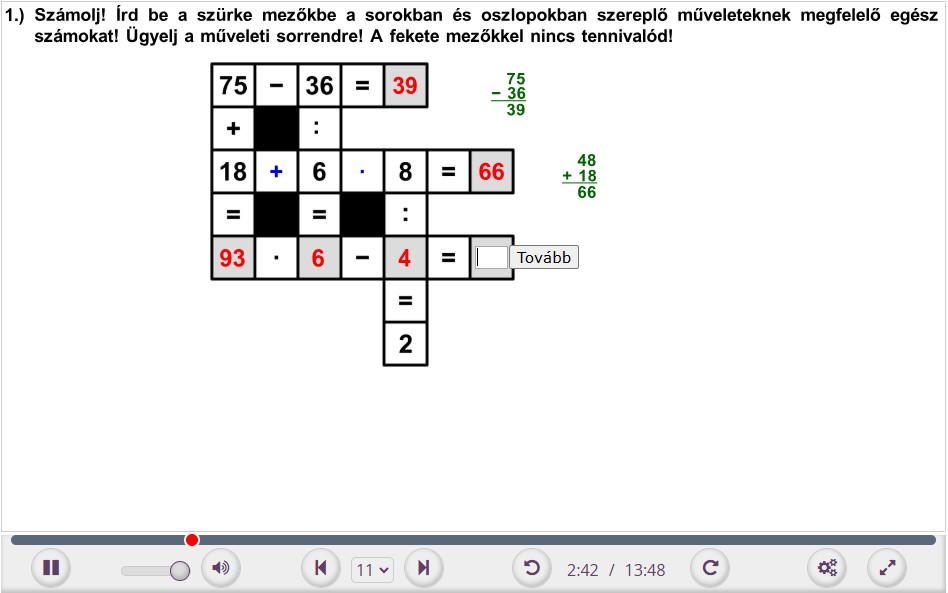
1. Számolj! Írd be a szürke mezőkbe a sorokban és oszlopokban szereplő műveleteknek megfelelő egész számokat! Ügyelj a műveleti sorrendre! A fekete mezőkkel nincs tennivalód.
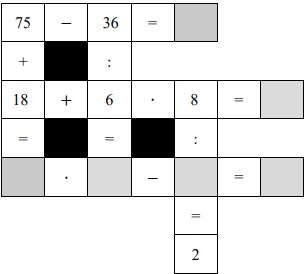
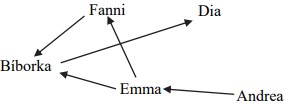
2. a) Öt fiú magasságát mutatja az ábra. Ennek alapján válaszolj a kérdésekre!
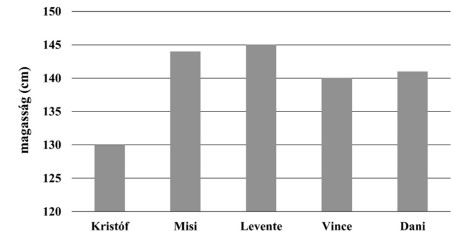
- Ha magasságuk szerint sorrendbe állnak a fiúk, ki van középen?
- Hány cm a különbség Vince és Kristóf magassága között?
3. Anna a következő négy számot írta fel:
615 399 1018 124
Add meg az állításoknak megfelelő számokat!
a) Anna legnagyobb páratlan számának százasokra kerekített értéke: …………….
b) Anna legnagyobb számánál 318-cal kisebb szám: …………….
c) Anna legkisebb számának tízszerese: …………….
d) Anna számai közül annak a harmada, amelyben a számjegyek összege 21: ……………
4. Az 536 olyan háromjegyű szám, melyre ezek az állítások igazak:
- második számjegye 2-vel kisebb az elsőnél,
- a harmadik számjegye pedig a második számjegy kétszerese.
5. Ákos, Leó és Misi unokatestvérek. Mindhármuknak különböző fajta kutyája van: vagy egy tacskó, vagy egy puli, vagy egy vizsla. A kutyák nevei: Lédi, Bogáncs és Picur. Az állítások alapján találd ki, hogy melyik gyereknek milyen fajtájú kutyája van és mi a kutya neve!
- Ákos kutyusa nem a tacskó és nem a vizsla.
- A pulit Bogáncsnak hívják.
- Leó kutyája nem a tacskó.
- Nem a tacskót hívják Lédinek.

6. Végezd el az átváltásokat!
a) 15 liter = ………………. dl
b) Fél km = ………………. m
c) 400 dkg = ………………. kg
d) 1 és negyed óra = ………………. perc
e) 30 dm + 6 cm = ………………. cm
7.
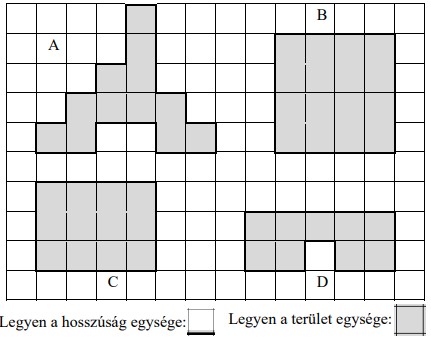
a) Az ábrán látható alakzatok közül melyekre igazak az állítások? Add meg a betűjelét! Figyelj, a rossz megoldásért pontlevonás jár!
Területe megegyezik a C jelű alakzat területével: …………………………
Van szimmetriatengelyük: …………………………
A legnagyobb területű alakzat: …………………………
b) Hány egység hosszú a D jelű alakzat kerülete? …………………………
8. 1 cm élű kis kockákból 4 cm élű nagyobb tömör kockát építettünk, majd a nagyobb kocka minden lapját különböző színűre festettük. Válaszolj a kérdésekre!
a) Hány kis kockára volt szükségünk? ………
b) Hány színt használtunk? ………
c) Hány olyan kis kocka van, amelynek pontosan három lapját festettük be? ………
d) Hány olyan kis kocka van, melynek minden lapját befestettük? ………

9. Három testvér közül Panka 7, Zoli 11, Peti pedig 13 éves.
a) 1 év múlva hány évesek lesznek összesen? …………………………
b) Amikor Zoli 20 éves lesz, hány éves lesz Panka? ……………………
c) Hány év múlva lesz Zoli és Peti életkorának összege 36 év? …………………….
Peti és Zoli ugyanannyi pénzt kapnak hetente. Panka 600 Ft-ot kap hetente, ami éppen a harmada annak, amit a két fiú kap összesen.
d) Mennyi zsebpénzt kapnak fejenként hetente a fiúk? …………………… Ft
Panka szeretne az édesanyjának egy karkötőt venni karácsonyra. Ezért minden héten félretesz 200 Ft-ot a zsebpénzéből.
e) Mennyibe került a karkötő, ha Panka 12 hétig gyűjtött rá és a fiúktól még kapott kölcsön összesen 500 Ft-ot? …………………… Ft
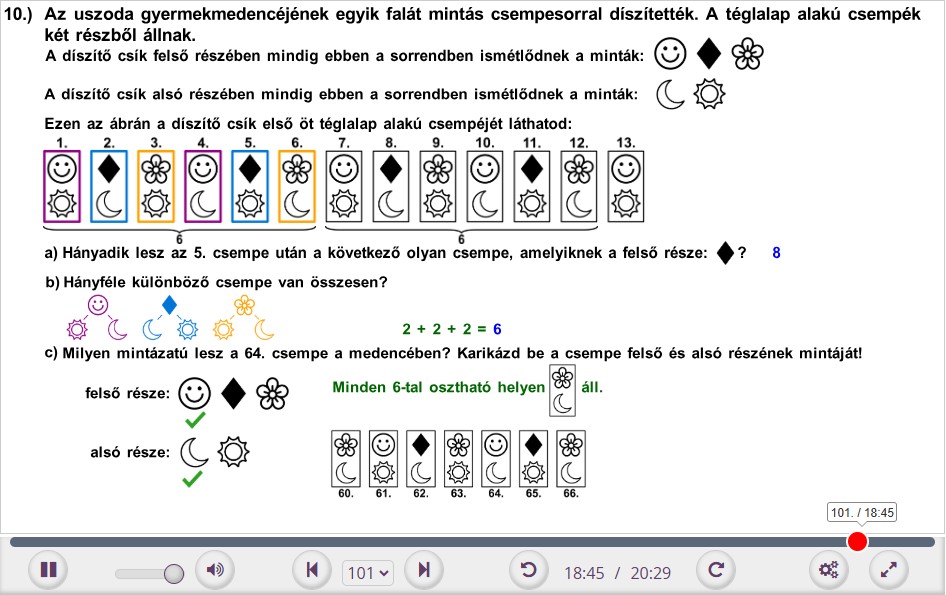
10. Az uszoda gyerekmedencéjének egyik falát mintás csempesorral díszítették. A téglalap alakú csempék két részből állnak.
A díszítő csík felső részében mindig ebben a sorrendben ismétlődnek a minták:

A díszítő csík alsó részében mindig ebben a sorrendben ismétlődnek a minták:

a) Hányadik lesz az 5. csempe után a következő olyan csempe, amelyiknek a felső része 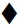 ?
?
b) Hányféle különböző csempe van összesen?
c) Milyen mintázatú lesz a 64. csempe a medencében? Karikázd be a csempe felső és alsó részének mintáját!
felső része: 
alsó része: 
A medence egyik falán a díszítő csíkot 115 csempe alkotja (a fenti sorminta szerint).
d) A csempék 2 dm szélesek. Hány méter hosszú ez a díszítő csík, ha a hosszabbik oldaluk mentén szorosan egymás mellé rakták őket?
Készítettünk egy egész tréninget, amivel felkészülhetsz egy sikeres felvételire! A tréning különleges felépítésének köszönhetően gyorsan tudsz fejlődni a felvételi feladatok megoldásában. Nézz bele ezekbe a tananyagokba is!
Többet szeretnék tudni a felvételi tréningről
Kapcsolódó tudástár tartalmak és blog bejegyzések
Középiskolai felvételi feladatok megoldásokkal 4., 6. és 8. osztályosoknak
[Manna FM rádió riport:] Középiskolai felvételi - A sikeres felkészülésről beszélgettünk
TV2 Életmódi: A középiskolai felvételi felkészülésről
Gimnáziumi felvételi: 3 gyakori tévhit!!!
RTL Klub Reggeli: Felvételi kevesebb stresszel és frusztrációval
Mitől nehéz a gimnáziumi felvételi vizsga, és hogyan lehet eredményesen felkészülni rá?
Sikerrecept a 8.-os felvételihez
Nyári recept a sikeres matek felvételihez
7 lépéses helyzetgyakorlat, amitől sokkal jobban sikerül a felvételid

Matek- és fizikatanár

Nehezen megy gyermekednek a szorzótábla? Elmondjuk miért!
Számos szülő számolt be arról, hogy mennyi nehézséget okozott a gyereknek (és így neki is) a szorzótáblák tanulása. Pedig régen mindenki tudta!