Lineáris függvény
Lineáris függvénynek nevezzük azt a függvényt, aminek a képe egyenes.
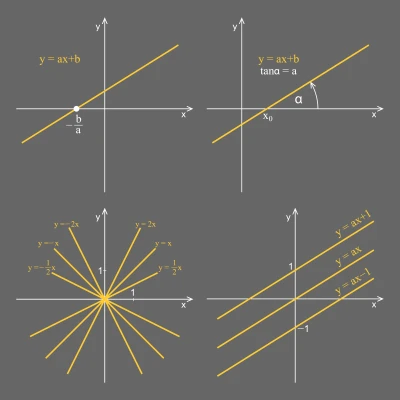
A hozzárendelési szabály általános alakja: f (x) = m · x + b.
Ebben az összefüggésben m a meredekség, b pedig azt jelöli, hogy a függvény hol halad át az y tengelyen. Ezeket két példán keresztül részletesen bemutatjuk.
Példa a lineáris függvények ábrázolására
Legyen f (x) = - x - 3; és g (x) = 
x + 2. Ábrázoljuk ezt a két függvényt közös koordinátarendszerben!
A lineáris függvény grafikonjának jellemzői:
- Meredekség: A függvény meredkségét m-mel jelöljük (az f (x) függvény esetén ez -1, a g (x) esetén ez ). A meredekség azt jelenti, hogy a grafikon egyik pontjából úgy kapunk meg egy másikat, hogy jobbra 1-et és fel/le "m" egységet lépünk.
Ha m > 0, akkor felfelé, ilyenkor növekvő a függvény
Ha m < 0, akkor lefelé, ekkor csökkenő a függvény.
Ha m ≠ 0, akkor a lineáris függvényt elsőfokú függvénynek nevezzük, hiszen a változó (x) első hatványon szerepel. Az egyenes az y tengelyt b-nél metszi.
Tehát: f (x) = -x - 3 esetén: m = -1 a meredekség és b = - 3 az y tengellyel vett tengelymetszet.
Tehát az ábrázolást kezdhetjük azzal, hogy az y tengelyen a -3-at bejelöljük, ez biztosan pontja a grafikonnak. Ezután innen lépegetünk tovább: Jobbra 1-et és le 1-et, így kapjuk meg az egyenesünk további pontjait .
Ha a meredekség nem egész, akkor ahhoz, hogy egész értékeket kapjunk, azaz rácspontokon lépdelhessünk, a következő módszert érdemes használni:
Például: f (x) =
x, akkor az origóból jobbra 2-t és le (a negatív előjel miatt) 1-et lépünk, hogy megkapjuk akövetkező pontot.
A következő Matek Oázis videókkal tanulhatsz a lineáris függvényről
Fontosabb függvények
Ezen a matematikai oktatóvideón a fontosabb függvénytípusokat vesszük sorra: lineáris függvények, másodfokú függvények, hatványfüggvények, abszolútérték-függvény, négyzetgyökfüggvény, és a törtfüggvények. Hogyan kell ábrázolni ezeket a függvényeket? Mi jellemzi őket szélsőérték, monotonitás, zérushely szempontjából, páros vagy páratlan-e a függvény.
Elsőfokú függvények - alapok
Bevezetünk a függvények világába. Lineáris függvényeket ábrázolunk koordináta-rendszerben: grafikonjuk egyenes f(x) = ax + b , ahol a a meredekség, és b-ben metszi az y-tengelyt; b=0 esetén az origó a függvénypontjuk. Megmutatjuk a lépkedéses módszert és az értéktáblázatot. Példákkal gyakorlunk.
Függvényábrázolás és jellemzés gyakorlása I. rész
Feladatok megoldásával gyakorold a függvények ábrázolását, függvényjellemzést és a függvénytranszformálást. Lineáris függvény, másodfokú függvény, hatványfüggvény, abszolútérték függvény, négyzetgyök függvény, törtfüggvény, páros ás páratlan függvény is előfordul a feladatokban. Segítünk, hogy mindezt megértsd.
Függvényábrázolás és jellemzés gyakorlása II. rész
Függvények ábrázolását, függvényjellemzést és a függvénytranszformálást is tudod gyakorolni ebben a tananyagban. Lineáris függvény, másodfokú függvény, hatványfüggvény, abszolútérték függvény, négyzetgyök függvény, törtfüggvény, páros ás páratlan függvény is előfordul a feladatokban.
